- What permissions do you give others to modify and/or maintain your submission?
- Modify: YES - Maintain: YES - I give permission for my entire submission to be modified by others or used in their own work. I give permission for my entire submission to be maintained by others as well.
- I made sure my file(s) follow the Submissions Guidelines
- Yes
- I named my file(s) correctly (see Filename Conventions)
- Yes
commandqueue!
commandqueue adds a suite of features which improves QoL for community kart servers, without modifying gameplay elements.
Features
suggestq
It's like "Add To Queue" from spotify, but in kart! All players can suggest to play a map next using this command. If the vote succeeds, that map will be played next without any voting phase. Now players can make requests for specific maps without needing to bother an admin!
How to use
In console (press ~), type
Note: you can suggest a map with its name, MapID, or two character code
If the vote passes, that map will be played next!
Note: Multiple maps can be queued at once, so feel free to keep queuing up as much as you want!
Server owner notes
* This feature requires hostmod to be loaded on your server
* You will need to make
* Additionally, you'll need to enable the commandqueue, and poponvote cvars:
* Also, you will need to whitelist the
Queuing up a whole cup
With just one command, you can queue up an entire cup to automatically play on your server
When the following command is issued, the first four maps of the game will be played in order. You can replace 01 etc with any map ID, and you can add as many or few IDs as you'd like.
Note: You'll need to have the following commands in your kartserv.cfg in order to have this work:
Other features
You can queue up any command. So in theory you can queue up anything as long as you whitelist it. (To whitelist a command issue
To have scores be cleared in 3 races:
To hold a particular character event:
To hold a tournament with a particular set of maps:
Note: ATO now does this better. Though similar functionality can be achieved here too
Have the server do an action every n rounds:
You can alias a command with addq in it. If that alias refers to itself, it will continuously queue that command. Building off of the clearscores example, let's have the server issue clearscores every 3 rounds:
To start it, now issue the alias:
You will need to whitelist each of these commands
Do NOT create an alias which is 2 letters long - this will confuse commandqueue at it assumes all 2 letter codes are maps.
Congratulations, you have now automated your server without any 'code'
Your imagination is the limit
Above are examples which use commands that come with vanilla kart. But you can put any custom command or alias in to be queued. So go nuts. There's a lot of different settings you can adjust in an automated fashion. Good luck!
Server setup
Commandqueue is disabled by default. To enable, turn on, the 2 added console vars. Then whitelist the commands you would like to queue. In your kartserv.cfg add the following commands:
* Some commands are perma-blacklisted e.g. promote as they should never be queued
Full command list
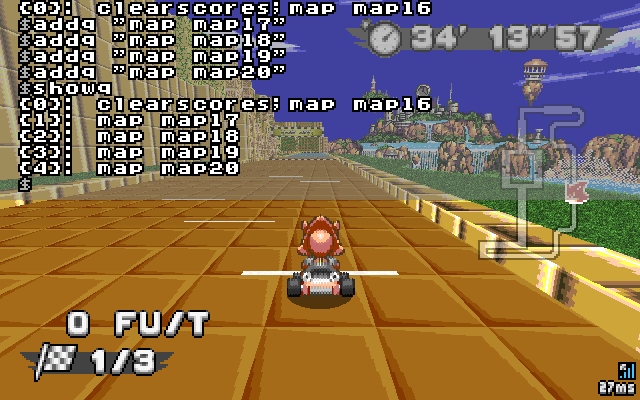
Image: showq usage:
Acknowledgements
Tyron and co-authors of hostmod. Several components were re-used in this mod.
commandqueue adds a suite of features which improves QoL for community kart servers, without modifying gameplay elements.
Features
suggestq
It's like "Add To Queue" from spotify, but in kart! All players can suggest to play a map next using this command. If the vote succeeds, that map will be played next without any voting phase. Now players can make requests for specific maps without needing to bother an admin!
How to use
In console (press ~), type
suggestq followed by the name of your desired mapNote: you can suggest a map with its name, MapID, or two character code
suggestq Coastal Templesuggestq MAP57suggestq 57If the vote passes, that map will be played next!
Note: Multiple maps can be queued at once, so feel free to keep queuing up as much as you want!
Server owner notes
* This feature requires hostmod to be loaded on your server
* You will need to make
addq votable with hostmod. Add in your kartserv.cfg the following: hm_votable addq* Additionally, you'll need to enable the commandqueue, and poponvote cvars:
cq_commandqueue 1cq_poponvote 1* Also, you will need to whitelist the
map commandcq_whitelist mapQueuing up a whole cup
With just one command, you can queue up an entire cup to automatically play on your server
addq 01 02 03 04When the following command is issued, the first four maps of the game will be played in order. You can replace 01 etc with any map ID, and you can add as many or few IDs as you'd like.
Note: You'll need to have the following commands in your kartserv.cfg in order to have this work:
cq_commandqueue 1cq_poponvote 1cq_whitelist mapOther features
You can queue up any command. So in theory you can queue up anything as long as you whitelist it. (To whitelist a command issue
cq_whitelist <command>)To have scores be cleared in 3 races:
addq "";addq ""; addq clearscoresTo hold a particular character event:
addq "forceskin aiai";addq "forceskin off"To hold a tournament with a particular set of maps:
Note: ATO now does this better. Though similar functionality can be achieved here too
clearscores;addq 01 02 03 04 05Have the server do an action every n rounds:
You can alias a command with addq in it. If that alias refers to itself, it will continuously queue that command. Building off of the clearscores example, let's have the server issue clearscores every 3 rounds:
alias css "clearscores;addq wait;addq wait; addq css"To start it, now issue the alias:
cssYou will need to whitelist each of these commands
cq_whitelist addqcq_whitelist waitcq_whitelist cssDo NOT create an alias which is 2 letters long - this will confuse commandqueue at it assumes all 2 letter codes are maps.
Congratulations, you have now automated your server without any 'code'
Your imagination is the limit
Above are examples which use commands that come with vanilla kart. But you can put any custom command or alias in to be queued. So go nuts. There's a lot of different settings you can adjust in an automated fashion. Good luck!
Server setup
Commandqueue is disabled by default. To enable, turn on, the 2 added console vars. Then whitelist the commands you would like to queue. In your kartserv.cfg add the following commands:
cq_commandqueue 1 enables all commands in the modcq_poponvote 1 Will now automatically execute popq on the first frame of the vote screen. popq description below.cq_whitelist map The command "map" may now be queued. Replace map with any* you would like to queue.* Some commands are perma-blacklisted e.g. promote as they should never be queued
Full command list
| command | args | example | Description | |
| addq | "your command" | addq "forceskin aiai" | Adds "your command" to the queue. The command won't be executed immediately. Instead it goes into the queue, which will execute all the commands it sees in First-In-First-Out fashion | |
| popq | popq | Executes the next command in the queue. This is issued automatically after intermission when cq_poponvote is enabled. The command is subsequently removed from the queue. | ||
| showq | showq | Displays all commands currently in the queue. The next command is at index {0}. The one after at is at index {1}, and so on. See image below. | ||
| suggestq | map name | suggestq Green Hills | Calls a hostmod vote to add the provided map to the queue to be played. hm_votable addq must be issued before it can work. | |
| helpq | cq_command | helpq suggestq | Shows help for the specified command queue command. type it alone for the welcome message. | |
| addfrontq | "your
| addfrontq "map map28" | Adds "your command" to the front of the queue. Will execute next on popq. Good in an emergency situation. | |
| editq | index, "your command" | editq 1 "map map01" | Changes the command at the specified index to your new command. showq to view indexes. Warning: the command will be overwritten. insertq to instead add at this index. | |
| deleteq | index | deleteq 2 | Deletes the command at the specified index. showq to view indexes. | |
| insertq | index, "your command" | inesertq 1 "map mapHC" | Inserts "your command" before the command at the specified index. showq to view indexes. addfrontq simply calls "insertq 0 yourcommand". | |
| clearq | [-force] | clearq -force | Clears the entire queue. DANGER! Queue is not recoverable after this operation. As a result, -force must be provided to enact the action |
Image: showq usage:
Acknowledgements
Tyron and co-authors of hostmod. Several components were re-used in this mod.

